Warning

You are reading the documentation related to the development version. Go here if you are looking for the documentation of the stable release.

Note

Go to the end to download the full example code.

NDDataset baseline correction

In this example, we perform a baseline correction of a 2D NDDataset interactively, using the multivariate method and a pchip/polynomial interpolation.

For comparison, we also use the asls`and `snip models.

As usual we start by importing the useful library, and at least the spectrochempy library.

import spectrochempy as scp

Load data

datadir = scp.preferences.datadir
nd = scp.NDDataset.read_omnic(datadir / "irdata" / "nh4y-activation.spg")

Do some slicing to keep only the interesting region

ndp = nd[:, 1291.0:5999.0]
# Important:  notice that we use floating point number
# integer would mean points, not wavenumbers!

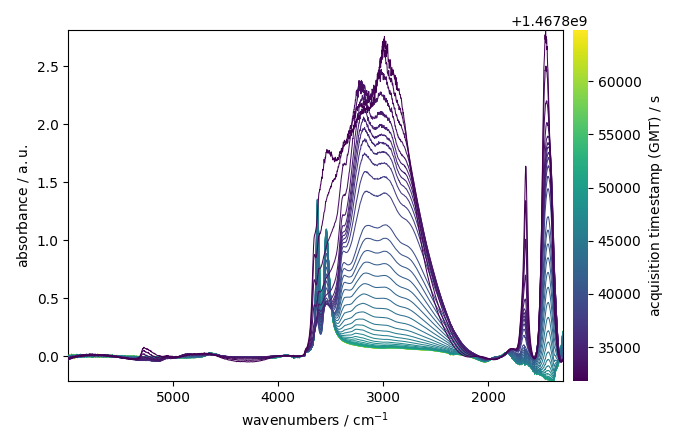
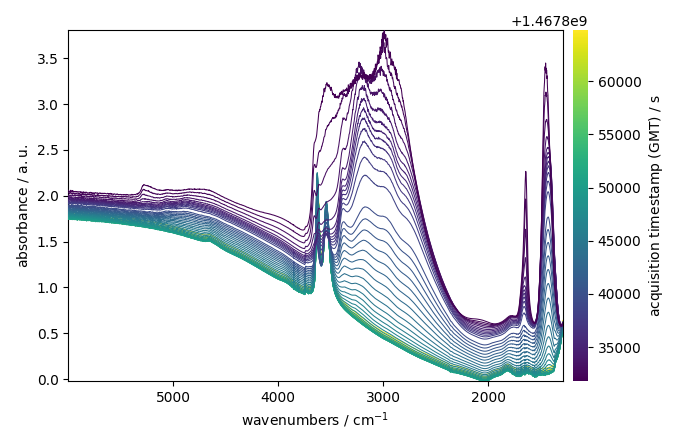
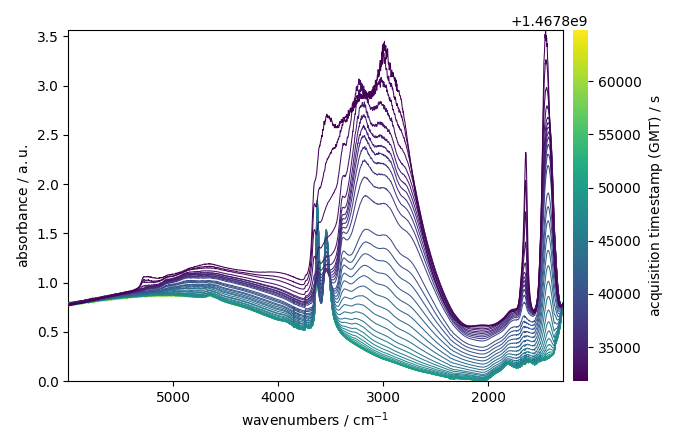
Plot the dataset

_ = ndp.plot()
plot baseline correction

Remove a basic linear baseline using basc:

ndp = ndp.basc()

Make it positive

offset = ndp.min()
ndp -= offset
_ = ndp.plot()
plot baseline correction

Define the Baseline object for a multivariate baseline correction model. The n_components parameter is the number of components to use for the multivariate baseline correction. The model parameter is the baseline correction model to use, here a pchip interpolation (piecewise cubic Hermite interpolation).

blc = scp.Baseline(
    log_level="INFO",
    multivariate=True,  # use a multivariate baseline correction approach
    model="polynomial",  # use a polynomial model
    order="pchip",  # with a pchip interpolation method
    n_components=5,
)

Now we select the regions ( ranges ) to use for the baseline correction.

blc.ranges = [
    [1556.30, 1568.26],
    [1795.00, 1956.75],
    [3766.03, 3915.81],
    [4574.26, 4616.04],
    [4980.10, 4998.01],
    [5437.52, 5994.70],
]

We can now fit the baseline correction model to the data:

_ = blc.fit(ndp)

The baseline is now stored in the baseline attribute of the processor: (note that the baseline is a NDDataset too). The corrected dataset (the dataset after the baseline subtraction) is stored in the corrected attribute of the processor:

baseline = blc.baseline
corrected = blc.corrected

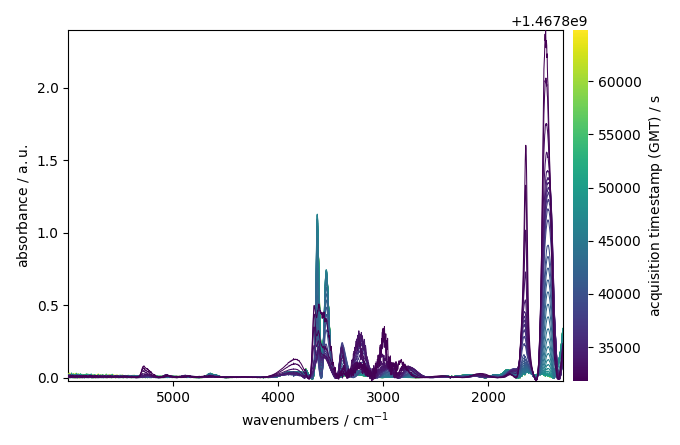
Plot the result of the correction

_ = corrected.plot()
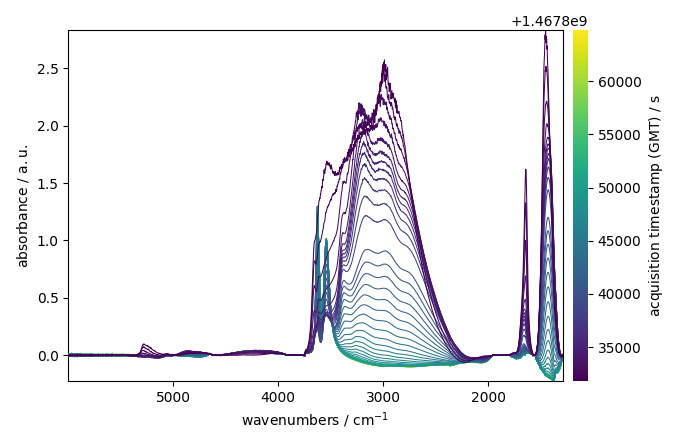
plot baseline correction

We can have a more detailed representation using plot

ax = blc.plot(nb_traces=2, offset=50)
blc.show_regions(ax)
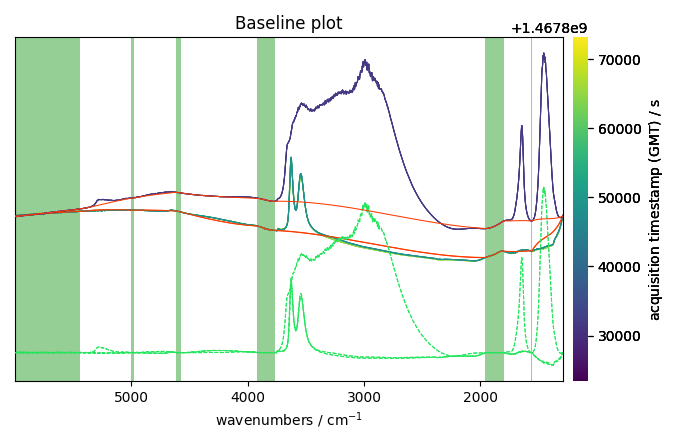
Baseline plot

We can also plot the baseline and the corrected dataset together: for some individual spectra to, for example, check the quality of the correction:

_ = corrected[0].plot()
_ = baseline[0].plot(clear=False, color="red", ls="-")
_ = ndp[0].plot(clear=False, color="green", ls="--")

_ = corrected[10].plot()
_ = baseline[10].plot(clear=False, color="red", ls="-")
_ = ndp[10].plot(clear=False, color="green", ls="--")
  • plot baseline correction
  • plot baseline correction

The baseline correction looks ok in some part of the spectra but not in others where the variation seems a little to rigid. This is may be due to the fact that the pchip interpolation is perhaps not the best choice for this dataset. We can try to use a n-th degree polynomial model instead:

We don’t need to redefine a new Baseline object, we can just change the model and the order of the polynomial:

blc.model = "polynomial"
blc.order = 5  # use a 5th degree polynomial

and fit again the baseline correction model to the data:

blc.fit(ndp)

baseline = blc.baseline
corrected = blc.corrected

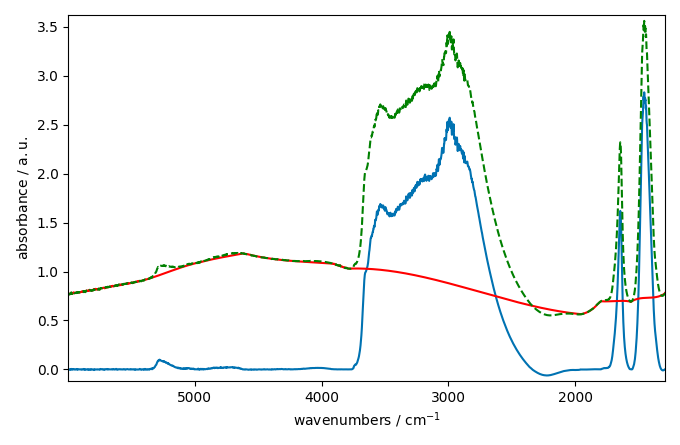
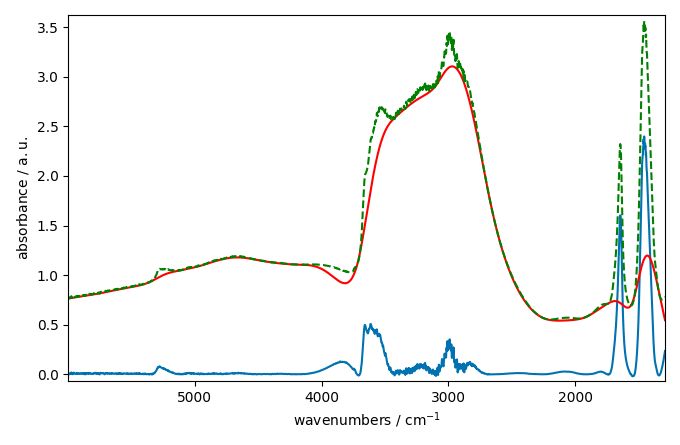
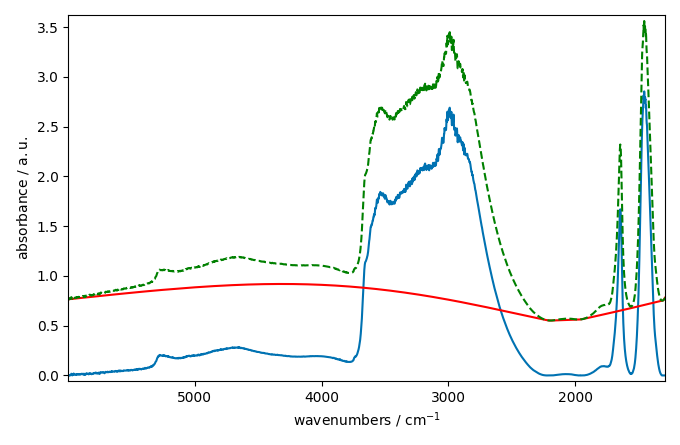
_ = corrected[0].plot()
_ = baseline[0].plot(clear=False, color="red", ls="-")
_ = ndp[0].plot(clear=False, color="green", ls="--")

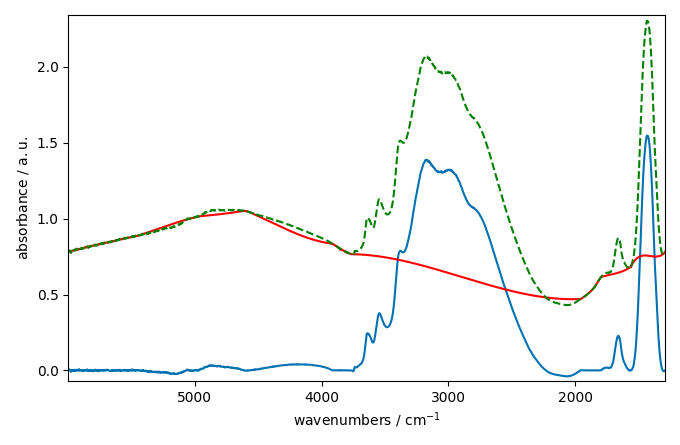
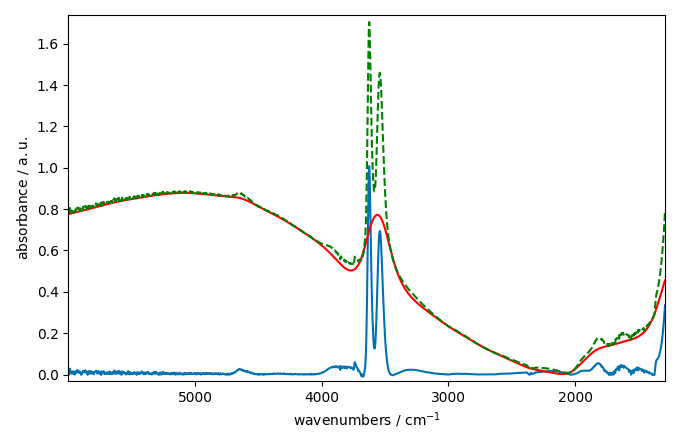
_ = corrected[10].plot()
_ = baseline[10].plot(clear=False, color="red", ls="-")
_ = ndp[10].plot(clear=False, color="green", ls="--")

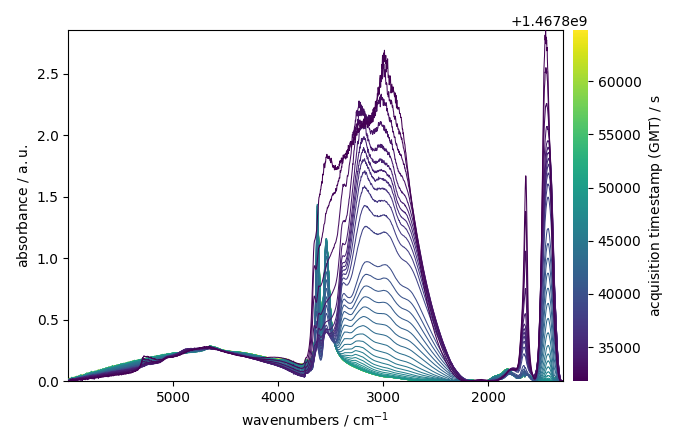
_ = corrected.plot()
  • plot baseline correction
  • plot baseline correction
  • plot baseline correction

This looks better and smoother. But not perfect.

We can also try to use a asls (Asymmetric Least Squares) model instead. This model is based on the work of Eilers and Boelens (2005) and performs a baseline correction by iteratively fitting asymmetrically weighted least squares regression curves to the data. The asls model has two parameters: mu and assymetry. The mu parameter is a regularisation parameters which control the smoothness of the baseline. The larger mu is, the smoother the baseline will be. The assymetry parameter is a parameter which control the assymetry if the AsLS algorithm.

blc.multivariate = False  # use a sequential approach
blc.model = "asls"
blc.mu = 10**9
blc.asymmetry = 0.002
blc.fit(ndp)

baseline = blc.baseline
corrected = blc.corrected

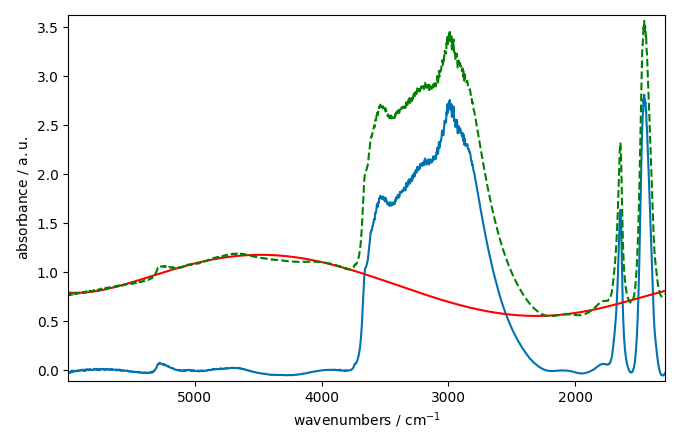
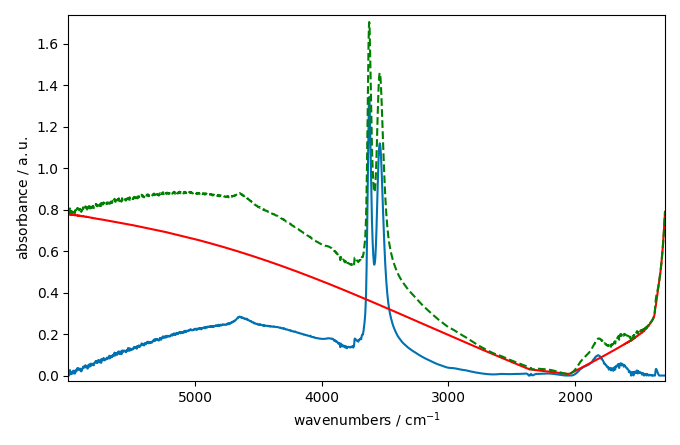
_ = corrected[0].plot()
_ = baseline[0].plot(clear=False, color="red", ls="-")
_ = ndp[0].plot(clear=False, color="green", ls="--")

_ = corrected[-1].plot()
_ = baseline[-1].plot(clear=False, color="red", ls="-")
_ = ndp[-1].plot(clear=False, color="green", ls="--")

_ = corrected.plot()
  • plot baseline correction
  • plot baseline correction
  • plot baseline correction
99999.49622650011
0.24660331763260296
0.14665656358795823
0.08444480851935286
0.0785295924636494
0.038550890845791524
0.02162113454843334
0.014278107720663527
0.012238378046283024
0.005915216055703461
0.005915216055703462
0.003875486381322957
0.0034675404464468568
0.004079459348761008
0.001019864837190252
0.0
Convergence reached in 15 iterations
99999.49133114889
0.2565979930370674
0.1413532664345689
0.0805693221380299
0.06241572803604341
0.037531026008601275
0.025088674994880197
0.006935080892893713
0.006935080892893713
0.006119189023141511
0.00530329715338931
0.003875486381322957
0.00550727012082736
0.0024476756092566047
0.0012238378046283023
0.00040794593487610074
Convergence reached in 15 iterations
99999.50234568912
0.24599139873028875
0.14441286094613967
0.0826090518124104
0.06282367397091952
0.04405816096661888
0.020397296743805037
0.01631783739504403
0.006731107925455663
0.008566864632398115
0.0034675404464468563
0.0028556215441327055
0.001427810772066353
0.0006119189023141512
Convergence reached in 13 iterations
99999.49133114889
0.2519066147859922
0.14176121236944503
0.08668851116117142
0.056704484947778015
0.04079459348761008
0.027128404669260704
0.015705918492729877
0.008158918697522015
0.009178783534712267
0.0036715134138849063
0.0012238378046283025
0.00040794593487610074
Convergence reached in 12 iterations
99999.49194306778
0.25027483104648784
0.13890559082531231
0.09219578128199876
0.053644890436207245
0.03181978292033587
0.024884702027442147
0.011626459143968872
0.010810567274216669
0.0069350808928937135
0.002039729674380504
0.0
Convergence reached in 11 iterations
99999.50724104035
0.24089207454433748
0.13706983411836987
0.0817931599426582
0.052013106696702845
0.03181978292033586
0.02100921564611919
0.013870161785787427
0.010402621339340569
0.0034675404464468563
0.001631783739504403
0.0
Convergence reached in 11 iterations
99999.49357485153
0.24741920950235513
0.13217448289985662
0.08281302477984845
0.046709809543313545
0.029984026213393408
0.022029080483309437
0.01672578332992013
0.011830432111406922
0.0044874052836371085
0.002039729674380504
0.00020397296743805037
Convergence reached in 11 iterations
99999.496838419
0.25517018226500104
0.13217448289985664
0.08240507884497236
0.05405283637108335
0.02366086422281384
0.02039729674380504
0.009994675404464469
0.009178783534712267
0.004691378251075159
0.0008158918697522015
Convergence reached in 10 iterations
99999.49928609462
0.24619537169772682
0.12544337497440097
0.07791767356133524
0.04854556625025599
0.019377431906614787
0.021009215646119187
0.010198648371902519
0.005711243088265411
0.007954945730083965
0.002651648576694655
0.0012238378046283023
0.0
Convergence reached in 12 iterations
99999.49765431088
0.25109072291624
0.1274831046487815
0.0805693221380299
0.04283432316199059
0.021417161580995294
0.03365553962727831
0.014890026622977677
0.006731107925455662
0.002651648576694655
0.001019864837190252
0.0
Convergence reached in 11 iterations
99999.49398279747
0.24293180421871802
0.1323784558672947
0.07689780872414499
0.03977472865041982
0.02039729674380504
0.028556215441327054
0.011830432111406922
0.006323161990579562
0.003875486381322957
0.00040794593487610074
Convergence reached in 10 iterations
99999.49581855418
0.2441556420233463
0.1323784558672947
0.06853491705918492
0.03793897194347737
0.025292647962318247
0.018765513004300637
0.009994675404464469
0.005711243088265411
0.0016317837395044032
0.00040794593487610074
Convergence reached in 10 iterations
99999.49847020274
0.23742453409789066
0.129522834323162
0.0797534302682777
0.04344624206430473
0.029576080278517308
0.013666188818349375
0.00550727012082736
0.005711243088265411
0.002039729674380504
0.0006119189023141512
Convergence reached in 10 iterations
99999.49337087855
0.23660864222813846
0.13401023960679911
0.07812164652877329
0.039570755682981774
0.031003891050583657
0.01631783739504403
0.008158918697522015
0.0044874052836371085
0.0034675404464468563
0.0006119189023141512
Convergence reached in 10 iterations
99999.49867417572
0.24130002047921362
0.129522834323162
0.07914151136596355
0.039774728650419824
0.030595945115707558
0.012442351013721074
0.008974810567274217
0.0048953512185132084
0.001631783739504403
0.00040794593487610074
Convergence reached in 10 iterations
99999.49622650011
0.24211591234896584
0.13135859103010444
0.08118124104034405
0.047729674380503795
0.02692443170182265
0.010810567274216669
0.007954945730083965
0.0028556215441327055
0.0014278107720663525
0.00040794593487610074
Convergence reached in 10 iterations
99999.49643047307
0.24517550686053655
0.13523407741142743
0.08260905181241042
0.041814458324800324
0.0267204587343846
0.011626459143968872
0.008362891664960065
0.002039729674380504
0.0006119189023141512
Convergence reached in 9 iterations
99999.49602252714
0.24354372312103217
0.13033872619291417
0.08995207864018022
0.04018267458529593
0.025088674994880197
0.012646323981159124
0.008566864632398115
0.003671513413884907
0.0018357567069424532
0.00020397296743805037
Convergence reached in 10 iterations
99999.49439074339
0.25313045259062056
0.1266672127790293
0.07322629531026009
0.04772967438050378
0.025088674994880197
0.013054269916035224
0.004691378251075159
0.003059594511570756
0.001019864837190252
0.00040794593487610074
Convergence reached in 10 iterations
99999.50356952693
0.25863772271144786
0.12381159123489659
0.07322629531026009
0.043242269096866674
0.023864837190251897
0.009790702437026419
0.00530329715338931
0.002039729674380504
0.00040794593487610074
Convergence reached in 9 iterations
99999.50234568912
0.25251853368830635
0.1344181855416752
0.06914683596149908
0.04385418799918083
0.03161580995289781
0.015501945525291829
0.004895351218513209
0.0018357567069424536
0.00040794593487610074
Convergence reached in 9 iterations
99999.50010198649
0.25353839852549664
0.13747778005324596
0.07648986278926889
0.04405816096661888
0.02345689125537579
0.012646323981159122
0.00550727012082736
0.002447675609256605
0.0012238378046283025
0.0
Convergence reached in 10 iterations
99999.51030063485
0.26026950645095226
0.12972680729060004
0.06812697112430882
0.04446610690149498
0.02243702641818554
0.011830432111406922
0.0069350808928937135
0.002039729674380504
0.00020397296743805037
Convergence reached in 9 iterations
99999.50152979726
0.2555781281998771
0.1340102396067991
0.06486340364530002
0.039774728650419824
0.03712308007372517
0.01631783739504403
0.008974810567274217
0.003875486381322957
0.00040794593487610074
Convergence reached in 9 iterations
99999.51601187795
0.2512946958836781
0.13217448289985664
0.06629121441736636
0.037123080073725175
0.03528732336678271
0.015501945525291829
0.013462215850911324
0.012442351013721074
0.004079459348761008
0.001019864837190252
0.0
Convergence reached in 11 iterations
99999.50887282408
0.25843374974400984
0.13013475322547613
0.0797534302682777
0.037123080073725175
0.04120253942248618
0.017541675199672334
0.02121318861355724
0.02284497235306164
0.01081056727421667
0.00530329715338931
0.0018357567069424536
0.00040794593487610074
Convergence reached in 12 iterations
99999.51132049969
0.2529264796231825
0.1299307802580381
0.0793454843334016
0.041406512389924224
0.040386647552733974
0.016521810362482077
0.022029080483309437
0.01917345893917673
0.006731107925455663
0.004079459348761008
0.002855621544132705
0.0006119189023141512
Convergence reached in 12 iterations
99999.51009666189
0.25251853368830635
0.12727913168134342
0.08362891664960066
0.049565431087446245
0.04772967438050379
0.022640999385623594
0.01611386442760598
0.008974810567274217
0.006323161990579562
0.005099324185951259
0.0028556215441327055
0.001019864837190252
0.00040794593487610074
Convergence reached in 13 iterations
99999.51662379685
0.2596575875486381
0.12707515871390537
0.08770837599836166
0.039978701617857874
0.03651116117141102
0.025496620929756297
0.014686053655539629
0.010198648371902519
0.005711243088265411
0.0034675404464468568
0.002855621544132705
0.002447675609256605
0.0006119189023141512
Convergence reached in 13 iterations
99999.51784763465
0.24089207454433748
0.13033872619291417
0.06649518738480444
0.07098259266844155
0.05854024165472045
0.03222772885521196
0.01733770223223428
0.008362891664960067
0.007954945730083967
0.004283432316199058
0.003875486381322957
0.0034675404464468568
0.0018357567069424536
0.0008158918697522015
Convergence reached in 14 iterations
99999.51621585092
0.24599139873028875
0.14196518533688307
0.05854024165472045
0.05609256604546385
0.04324226909686668
0.023456891255375794
0.017949621134548434
0.008770837599836167
0.008974810567274217
0.00550727012082736
0.00530329715338931
0.003671513413884907
0.0024476756092566047
0.002039729674380504
0.0008158918697522015
Convergence reached in 15 iterations
99999.51927544542
0.2527225066557444
0.13135859103010444
0.062007782101167315
0.06200778210116732
0.04385418799918083
0.024476756092566044
0.01652181036248208
0.010606594306778622
0.0071390538603317635
0.006527134958017612
0.0044874052836371085
0.0046913782510751584
0.002039729674380504
0.00020397296743805037
Convergence reached in 14 iterations
99999.51560393201
0.24497153389309853
0.14094532049969283
0.07037067376612738
0.05486872824083556
0.039570755682981774
0.018357567069424534
0.023660864222813844
0.011626459143968872
0.013258242883473277
0.005915216055703461
0.00489535121851321
0.002855621544132705
0.004283432316199058
0.001631783739504403
0.0006119189023141512
Convergence reached in 15 iterations
99999.51907147246
0.2490509932418595
0.13095064509522836
0.06486340364530002
0.04222240425967643
0.03467540446446856
0.037123080073725175
0.01631783739504403
0.010606594306778622
0.00530329715338931
0.006527134958017612
0.005303297153389311
0.003671513413884907
0.0034675404464468563
0.002039729674380504
0.001019864837190252
0.00020397296743805037
Convergence reached in 16 iterations
99999.51580790499
0.24884702027442143
0.1368658611509318
0.06363956584067172
0.06098791726397707
0.046709809543313545
0.02896416137620315
0.019989350808928937
0.008362891664960065
0.006119189023141511
0.00550727012082736
0.00489535121851321
0.003671513413884907
0.003263567479008806
0.0008158918697522015
Convergence reached in 14 iterations
99999.51723571574
0.25394634446037273
0.13421421257423713
0.06547532254761418
0.051605160761826745
0.038142944910915424
0.03528732336678272
0.013666188818349375
0.012850296948597175
0.007343026827769813
0.0075469997952078635
0.005915216055703461
0.0028556215441327055
0.00489535121851321
0.001631783739504403
0.00020397296743805037
Convergence reached in 15 iterations
99999.51376817531
0.2604734794183903
0.13543805037886547
0.06343559287323366
0.05201310669670285
0.04099856645504813
0.038550890845791524
0.01713372926479623
0.008362891664960065
0.006731107925455663
0.007546999795207864
0.005099324185951259
0.004895351218513209
0.002855621544132705
0.0008158918697522015
Convergence reached in 14 iterations
99999.51478804015
0.2517026418185541
0.13625394224861764
0.07669383575670694
0.04854556625025599
0.040386647552733974
0.04018267458529593
0.01611386442760598
0.011014540241654722
0.006527134958017611
0.007139053860331762
0.005915216055703462
0.0018357567069424536
0.005099324185951259
0.002039729674380504
0.00020397296743805037
Convergence reached in 15 iterations
99999.51397214826
0.2574138849068196
0.14155723940200696
0.06261970100348146
0.04467007986893304
0.058744214622158515
0.02733237763669875
0.017745648167110387
0.011014540241654722
0.009586729469588367
0.006527134958017612
0.004691378251075159
0.002855621544132705
0.0034675404464468563
0.001631783739504403
0.00040794593487610074
Convergence reached in 15 iterations
99999.52539463446
0.25211058775343026
0.13870161785787424
0.06996272783125128
0.038550890845791524
0.041202539422486174
0.03283964775752612
0.015297972557853779
0.013666188818349375
0.008158918697522015
0.007954945730083967
0.005099324185951259
0.004283432316199058
0.0022437026418185542
0.002855621544132705
0.001019864837190252
0.00020397296743805037
Convergence reached in 16 iterations
99999.51397214828
0.2553741552324391
0.1429850501740733
0.06608724144992832
0.042018431292238374
0.047117755478189645
0.036715134138849075
0.012850296948597175
0.012850296948597174
0.0069350808928937135
0.00530329715338931
0.006119189023141511
0.004283432316199058
0.003875486381322957
0.003263567479008806
0.001631783739504403
0.0
Convergence reached in 16 iterations
99999.52498668851
0.25394634446037273
0.13808969895556011
0.06731107925455662
0.04222240425967643
0.03406348556215441
0.042018431292238374
0.01754167519967233
0.008770837599836167
0.009178783534712267
0.006323161990579561
0.005915216055703461
0.0030595945115707555
0.0044874052836371085
0.0014278107720663525
0.00020397296743805037
Convergence reached in 15 iterations
99999.52090722918
0.2498668851116117
0.1429850501740733
0.061191890231415115
0.048953512185132095
0.05364489043620726
0.04568994470612329
0.01835756706942453
0.008974810567274217
0.009994675404464467
0.006323161990579562
0.006935080892893713
0.00571124308826541
0.002651648576694655
0.003671513413884907
0.0008158918697522015
Convergence reached in 15 iterations
99999.50968871596
0.26006553348351424
0.14237313127175918
0.06445545771042394
0.042630350194552524
0.04528199877124719
0.03426745852959247
0.016521810362482077
0.012850296948597175
0.0071390538603317635
0.008974810567274217
0.0046913782510751584
0.003671513413884907
0.00571124308826541
0.0012238378046283023
0.00020397296743805037
Convergence reached in 15 iterations
99999.51621585092
0.2602695064509523
0.1454327257833299
0.06731107925455662
0.04140651238992423
0.05323694450133115
0.027740323571574854
0.027740323571574854
0.014278107720663527
0.01060659430677862
0.005711243088265411
0.005915216055703461
0.004079459348761008
0.005099324185951259
0.0014278107720663528
0.0006119189023141512
Convergence reached in 15 iterations
99999.52111120212
0.2541503174278108
0.14359696907638747
0.06527134958017612
0.04405816096661889
0.039774728650419824
0.037327053041163225
0.01672578332992013
0.014278107720663527
0.008158918697522015
0.007954945730083965
0.004691378251075159
0.0024476756092566047
0.0042834323161990585
0.0018357567069424536
0.0006119189023141512
Convergence reached in 15 iterations
99999.52437476961
0.2447675609256604
0.14074134753225476
0.06404751177554782
0.04467007986893304
0.039570755682981774
0.03487937743190662
0.015501945525291829
0.008566864632398115
0.008974810567274217
0.00571124308826541
0.0034675404464468568
0.003263567479008806
0.002651648576694655
0.00040794593487610074
Convergence reached in 14 iterations
99999.51968339135
0.25353839852549664
0.14563669875076798
0.07485807904976449
0.047729674380503795
0.03447143149703052
0.039774728650419824
0.018765513004300634
0.009790702437026419
0.007546999795207864
0.006527134958017612
0.00509932418595126
0.002855621544132705
0.004283432316199058
0.0018357567069424536
0.00040794593487610074
Convergence reached in 15 iterations
99999.50785295924
0.2725078844972353
0.14237313127175916
0.07546999795207865
0.04691378251075158
0.03569526930165882
0.04242637722711448
0.01835756706942453
0.008974810567274217
0.0071390538603317635
0.006527134958017611
0.00550727012082736
0.0018357567069424532
0.004283432316199058
0.001019864837190252
0.0
Convergence reached in 15 iterations
99999.52090722916
0.259045668646324
0.13747778005324596
0.06425148474298586
0.04650583657587549
0.04589391767356134
0.036919107106287125
0.023864837190251897
0.011422486176530822
0.008770837599836167
0.007750972762645915
0.005099324185951259
0.0024476756092566047
0.00530329715338931
0.001631783739504403
0.0008158918697522015
Convergence reached in 15 iterations
99999.51805160762
0.26067745238582835
0.1470645095228343
0.07383821421257424
0.039366782715543724
0.038550890845791524
0.038550890845791524
0.020193323776366987
0.012442351013721074
0.007546999795207864
0.008974810567274217
0.006731107925455662
0.0034675404464468563
0.004691378251075159
0.0024476756092566047
0.00020397296743805037
Convergence reached in 15 iterations
99999.52049928323
0.26169731722301864
0.14196518533688307
0.06506737661273808
0.03773499897603932
0.03773499897603932
0.03814294491091543
0.01774564816711038
0.009586729469588367
0.0069350808928937135
0.00611918902314151
0.004079459348761008
0.003875486381322957
0.0022437026418185542
0.0030595945115707555
0.0006119189023141512
Convergence reached in 15 iterations
99999.51825558058
0.25394634446037273
0.14094532049969283
0.06669916035224248
0.04283432316199059
0.042630350194552524
0.029984026213393408
0.015501945525291825
0.013258242883473277
0.008158918697522015
0.0071390538603317635
0.00530329715338931
0.004079459348761008
0.003671513413884907
0.0014278107720663525
0.0
Convergence reached in 15 iterations
99999.5143800942
0.2541503174278108
0.14155723940200698
0.06853491705918492
0.04854556625025599
0.050177349989760395
0.0509932418595126
0.022844972353061644
0.009586729469588367
0.0075469997952078635
0.007139053860331764
0.00591521605570346
0.0024476756092566047
0.004895351218513209
0.0008158918697522015
Convergence reached in 14 iterations
99999.5119324186
0.25924964161376207
0.1454327257833299
0.06669916035224248
0.038754863813229574
0.043242269096866674
0.03691910710628712
0.01794962113454843
0.013054269916035224
0.006731107925455663
0.006527134958017612
0.00530329715338931
0.0022437026418185542
0.003263567479008806
0.0014278107720663525
0.00020397296743805037
Convergence reached in 15 iterations

Finally, we will use the snip model

blc.multivariate = False  # use a sequential approach
blc.model = "snip"
blc.snip_width = 200
blc.fit(ndp)

baseline = blc.baseline
corrected = blc.corrected

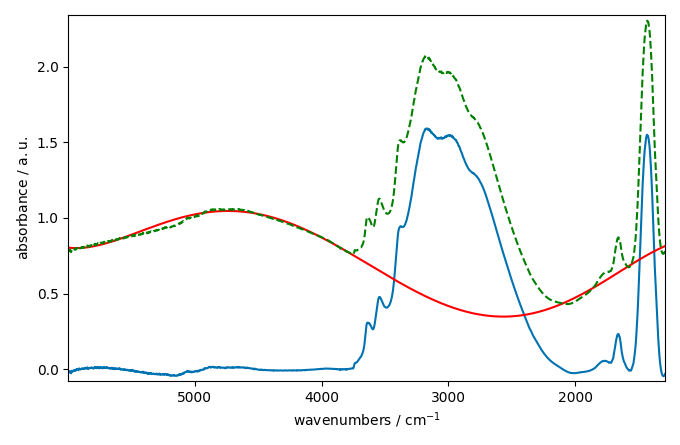
_ = corrected[0].plot()
_ = baseline[0].plot(clear=False, color="red", ls="-")
_ = ndp[0].plot(clear=False, color="green", ls="--")

_ = corrected[-1].plot()
_ = baseline[-1].plot(clear=False, color="red", ls="-")
_ = ndp[-1].plot(clear=False, color="green", ls="--")

_ = corrected.plot()
  • plot baseline correction
  • plot baseline correction
  • plot baseline correction

This ends the example ! The following line can be uncommented if no plot shows when running the .py script with python

# scp.show()

Total running time of the script: (0 minutes 7.070 seconds)