× ⚠️ You are reading the development version documentation.
Read here the documentation of the last stable release.

Peak Integration

This tutorial shows how to find peak maxima and determine peak areas with SpectroChemPy. As a prerequisite, the user is expected to have read the Import, Import IR, Slicing, and Baseline Correction tutorials.

First, let’s import the SpectroChemPy API.

import spectrochempy as scp

SpectroChemPy's API - v.0.8.2.dev7 ©Copyright 2014-2025 - A.Travert & C.Fernandez @ LCS

Now, import some 2D data into an NDDataset object.

ds = scp.read_omnic("irdata/nh4y-activation.spg")
ds

Running on GitHub Actions
MPL Configuration directory: /home/runner/.config/matplotlib
Stylelib directory: /home/runner/.config/matplotlib/stylelib

NDDataset: [float64] a.u. (shape: (y:55, x:5549))[nh4y-activation]

Summary

name

:

nh4y-activation

author

:

runner@fv-az2211-104

created

:

2025-04-27 01:45:18+00:00

description

:

Omnic title: NH4Y-activation.SPG
Omnic filename: /home/runner/.spectrochempy/testdata/irdata/nh4y-activation.spg

history

:

2025-04-27 01:45:18+00:00> Imported from spg file /home/runner/.spectrochempy/testdata/irdata/nh4y-activation.spg.
2025-04-27 01:45:18+00:00> Sorted by date

Data

title

:

absorbance

values

:

...

[[ 2.057 2.061 ... 2.013 2.012]
[ 2.033 2.037 ... 1.913 1.911]
...
[ 1.794 1.791 ... 1.198 1.198]
[ 1.816 1.815 ... 1.24 1.238]] a.u.

shape

:

(y:55, x:5549)

Dimension `x`

size

:

5549

title

:

wavenumbers

coordinates

:

[ 6000 5999 ... 650.9 649.9] cm⁻¹

Dimension `y`

size

:

55

title

:

acquisition timestamp (GMT)

coordinates

:

[1.468e+09 1.468e+09 ... 1.468e+09 1.468e+09] s

labels

:

...

[[ 2016-07-06 19:03:14+00:00 2016-07-06 19:13:14+00:00 ... 2016-07-07 04:03:17+00:00 2016-07-07 04:13:17+00:00]
[ vz0466.spa, Wed Jul 06 21:00:38 2016 (GMT+02:00) vz0467.spa, Wed Jul 06 21:10:38 2016 (GMT+02:00) ...
vz0520.spa, Thu Jul 07 06:00:41 2016 (GMT+02:00) vz0521.spa, Thu Jul 07 06:10:41 2016 (GMT+02:00)]]

It’s a series of 55 spectra.

For the demonstration, select only the first 20 on a limited region from 1250 to 1800 cm\(^{-1}\) (Do not forget to use floating numbers for slicing).

X = ds[:20, 1250.0:1800.0]

We can also eventually remove the offset on the acquisition time dimension (y).

X.y -= X.y[0]
X.y.ito("min")
X.y.title = "acquisition time"

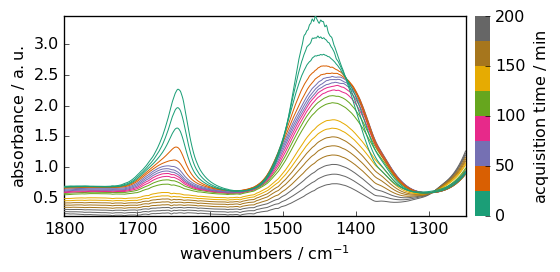
We set some plotting preferences and then plot the raw data.

prefs = scp.preferences
prefs.figure.figsize = (6, 3)
prefs.colormap = "Dark2"
prefs.colorbar = True
X.plot()

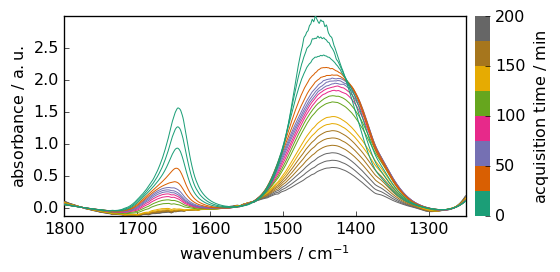
Now we can perform some baseline correction.

blc = scp.Baseline()
blc.ranges = (
    [1740.0, 1800.0],
    [1550.0, 1570.0],
    [1250.0, 1300.0],
)  # define 3 regions where we want the baseline to reach zero.
blc.model = "polynomial"
blc.order = 3

blc.fit(X)  # fit the baseline

Xcorr = blc.corrected  # get the corrected dataset
Xcorr.plot()

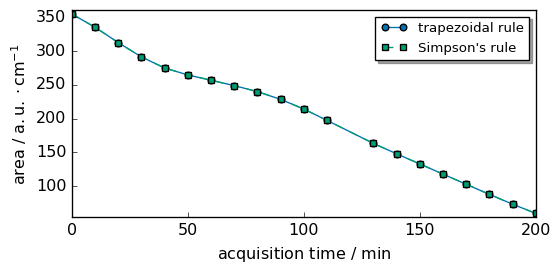
To integrate each row on the full range, we can use the sum or trapz method of an NDDataset.

inttrapz = Xcorr.trapezoid(dim="x")
intsimps = Xcorr.simpson(dim="x")

As you can see, both methods give almost the same results in this case.

scp.plot_multiple(
    method="scatter",
    ms=5,
    datasets=[inttrapz, intsimps],
    labels=["trapezoidal rule", "Simpson's rule"],
    legend="best",
)

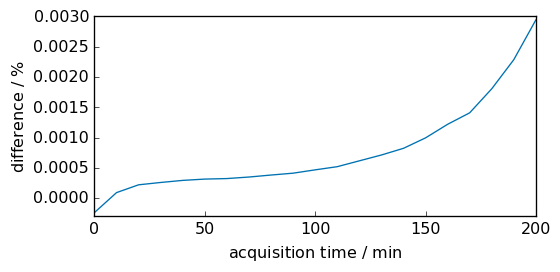
The difference between the trapezoidal and Simpson integration methods is visualized below. In this case, they are extremely close.

diff = (inttrapz - intsimps) * 100.0 / intsimps
diff.title = "difference"
diff.units = "percent"
diff.plot(scatter=True, ms=5)